How to avoid bias

Image credit: www.pixabay.com

Bayes Theorem

See this video on how Bayes' Theorem is derived:

Bayes' Theorem in 1 minute

Bayes Theorem makes use of conditional probability. See more in the video CRITICAL THINKING - Fundamentals: Bayes' Theorem [Length- 6:20]

Bayesian Approach

The beauty of the Bayesian Approach in Statistics allows us to update our prior knowledge based on evidence from data observed.

With applications in current topics such as artificial intelligence and neural networks; this definitely makes the Bayesian paradigm relevant and important. 

Follow the link below to an Analytics Vidyha blog post that gives us an introduction on Bayesian Statistics. But Bayesian Statistics cannot be explained without introducing the Frequentist view of probability first. See more in the blog post:

Bayesian Statistics explained to Beginners in Simple English

If  and  are two events then

can be written as

Application of Bayes Theorem

• Breathalysers display a false result in 5% of the cases tested
• They never fail to detect a truly drunk person
• 1/1000 of drivers are driving drunk
• Policemen then stop a driver at random, and test them
• The breathalyser indicates that the driver is drunk

What is the probability that a driver is drunk given that the breathalyser indicates that he/she is drunk?

Try this example and check if you reach the same conclusion as the Statistics for Decision Makers site by Bernard Szlachta.

When we alter the proportion of people that are sober as well as the error rate of the breathalyser test, we can reach an entirely different conclusion!

1. Introduction of the Law of Total Probability: 

so that

can be written as

and
 

2. Introduction of the likelihood function  _{which is the joint probability or probability density of all observations :}

Here Bayes Theorem has different notation on a continuous state space .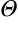

There is a difference between the Frequentist and Bayesian Approaches.

So it is important to know what each of these methods entail.

Examples are used in these videos in order to explain the differences between the two approaches:

It always seems impossible until it's done.

Nelson Mandela

This quote is a "Bayesian viewpoint of the world" according to the YouTube video The Bayesian Trap [Length- 10:36]

However The Bayesian Trap first focuses on these points:

• Bayes' Theorem interpretation when you test positive for a rare disease as well as how this probability changes if you get a second opinion
• History and origin of the theorem
• Practical application of Bayes in order to filter spam

Image credit: Mike Baldwin at https://www.flickr.com/photos/98471901@N00/15369286212